Neurevolution – Page 5 – Neuroscience, cognition, and society

Neural Network “Learning Rules”

Most neurocomputational models are not hard-wired to perform a task. Instead, they are typically equipped with some kind of learning process. In this post, I'll introduce some notions of how neural networks can learn. Understanding learning processes is important for cognitive neuroscience because they may underly the development of cognitive ability.

Let's begin with a theoretical question that is of general interest to cognition: how can a neural system learn sequences, such as the actions required to reach a goal?

Consider a neuromodeler who hypothesizes that a particular kind of neural network can learn sequences. He might start his modeling study by "training" the network on a sequence. To do this, he stimulates (activates) some of its neurons in a particular order, representing objects on the way to the goal.

After the network has been trained through multiple exposures to the sequence, the modeler can then test his hypothesis by stimulating only the neurons from the beginning of the sequence and observing whether the neurons in the rest sequence activate in order to finish the sequence.

Successful learning in any neural network is dependent on how the connections between the neurons are allowed to change in response to activity. The manner of change is what the majority of researchers call "a learning rule". However, we will call it a "synaptic modification rule" because although the network learned the sequence, it is not clear that the *connections* between the neurons in the network "learned" anything in particular.

The particular synaptic modification rule selected is an important ingredient in neuromodeling because it may constrain the kinds of information the neural network can learn.

There are many categories of mathematical synaptic modification rule which are used to describe how synaptic strengths should be changed in a neural network. Some of these categories include: backpropgration of error, correlative Hebbian, and temporally-asymmetric Hebbian.

Backpropogation of error states that connection strengths should change throughout the entire network in order to minimize the difference between the actual activity and the "desired" activity at the "output" layer of the network.
Correlative Hebbian states that any two interconnected neurons that are active at the same time should strengthen their connections, so that if one of the neurons is activated again in the future the other is more likely to become activated too.
Temporally-asymmetric Hebbian is described in more detail in the example below, but essentially emphasizes the importants of causality: if a neuron realiably fires before another, its connection to the other neuron should be strengthened. Otherwise, it should be weakened.

Why are there so many different rules? Some synaptic modification rules are selected because they are mathematically convenient. Others are selected because they are close to currently known biological reality. Most of the informative neuromodeling is somewhere in between.

An Example

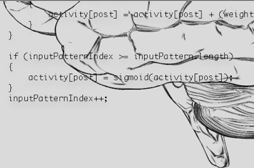
Let's look at a example of a learning rule used in a neural network model that I have worked with: imagine you have a network of interconnected neurons that can either be active or inactive. If a neuron is active, its value is 1, otherwise its value is 0. (The use of 1 and 0 to represent simulated neuronal activity is only one of the many ways to do so; this approach goes by the name "McCulloch-Pitts").

Continue reading “Neural Network “Learning Rules””

Predicting Intentions: Implications for Free Will

News about a neuroimaging group's attempts to predict intentions hit the wire a few days ago. The major theme was how mindreading might be used for unethical purposes.

What about its more profound implications?

If your intentions can be predicted before you've even made a conscious decision, then your will must be determined by brain processes beyond your control. There cannot be complete freedom of will if I can predict your decisions before you do!

Dr. Haynes, the researcher behind this work, spoke at Carnegie-Mellon University last October. He explained that he could use functional MRI to determine what participants were going to decide several seconds before that decision was consciously made. This was a free choice task, in which the instruction was to press a button whenever the participant wanted. In a separate experiment the group could predict if a participant was going to add or subtract two numbers.

In a way, this is not very surprising. In order to make a conscious decision we must be motivated by either external or internal factors. Otherwise our decisions would just be random, or boringly consistent. Decisions in a free choice task are likely driven by a motivation to move (a basic instinct likely originating in the globus pallidus) and to keep responses spaced within a certain time window.

Would we have a coherent will if it couldn't be predicted by brain activity? It seems unlikely, since the conscious will must use information from some source in order to make a reasoned decision. Otherwise we would be incoherent, random beings with no reasoning behind our actions.

In other words, we must be fated to some extent in order to make informed and motivated decisions.

-MC

Eliminating Common Misconceptions About fMRI

Most researchers in neuroscience use animal models.

Though most neuroscientists are interested in understanding the human brain, they can use more invasive techniques with animal brains. In exchange for these invasive abilities they must assume that other animals are similar enough to humans that they can actually learn something about humans in the process.

Functional magnetic resonance imaging (fMRI) is a non-invasive technique for measuring changes in local blood flow (which are significantly correlated with changes in neural activity) in the brain. fMRI measures what is called the blood oxygen level-dependent (BOLD) signal. Because it is non-invasive it can be used with human subjects.

Researchers like ourselves recognize the value of animal research, especially when the behavior being investigated is similar between the studied species and humans.

However, there is at least one fundamental cognitive difference between humans and all other animals, and likely many more given the dominant position of our species.
For researchers like ourselves it is much more interesting to learn something about the human brain (the item of interest) rather than, say, the rat brain.

Why do some neuroscientists think that using fMRI to study the neural basis of cognition in humans is of little value?

Many have heard that there are issues with fMRI as a technique. There are (like any technique), but not as many as most believe.

Here are some common misconceptions about fMRI:
Continue reading “Eliminating Common Misconceptions About fMRI”

Demystifying the Brain

Most neuroscience writing touts statements like 'the human brain is the most complex object in the universe'. This serves only to paint the brain as a mysterious, seemingly unknowable structure.

This is somehow comforting to some, but it's not for me. I want to understand this thing!

Here are some facts to demystify the brain (most points courtesy of Dave Touretzky and Christopher Cherniak):

The brain is very complex, but not infinitely so
A few spoonfuls of yogurt contain 10¹¹ lactobaccillus bacteria: ten times the number of cortical neurons in a human brain
There are roughly 10¹³ synapses in cortex. Assume each stores one bit of information: that’s 1.25 terabytes.

To put this in perspective, this 2.0 terabyte hard drive is readily available and costs less than $900.

Also, the Library of Congress (80 million volumes, average 300 typed pages each) contains about 48 terabytes of data.

Volume of the human brain: about 1.4 liters.
Number of neurons in a human brain: 10¹². Number of neurons in a rat brain: 10¹⁰.
Number of neurons in human spinal cord: 10⁹ [source]
Average loss of neocortical neurons = 1 per second; 85,000 per day; ~31 million (31×10⁶) per year [source]
No neuron fires faster than 1 kHz
The total energy consumption of the brain is about 25 watts [source]
Average number of glial cells in brain = 10-50 times the number of neurons [source]
"For all our neurocomputational sophistication and processing power, we can barely attend to more than one object at a time, and we can hardly perform two tasks at once" [source]

What to take from all this? Simply that the brain is a real, physical object with real, physical limitations. As such, we really do have a chance to understand it.

Of course, if the brain is so limited, how can we expect our brains to be up to the task of understanding it?

We can, and we will. How can I be so sure? Because (as illustrated above) we have already built, and thus understand, computational devices that are rivaling and in some cases surpassing (e.g., in memory capacity) the computational powers of the brain.

This shows that we have what it takes to understand ourselves in the deepest way possible: by learning the neural mechanisms that make us who and what we are.

-MC

Computational models of cognition in neural systems: WHY?

In my most recent post I gave an overview of the "simple recurrent network" (SRN), but I'd like to take a step back and talk about neuromodeling in general. In particular I'd like to talk about why neuromodeling is going to be instrumental in bringing about the cognitive revolution in neuroscience.

A principal goal of cognitive neuroscience should be to explain how cognitive phenomena arise from the underlying neural systems. How do the neurons and their connections result in interesting patterns of thought? Or to take a step up, how might columns, or nuclei, interact to result in problem solving skills, thought or consciousness?

If a cognitive neuroscientist believes they know how a neural system gives rise to a behavior, they should be able to construct a model to demonstrate how this is the case.

That, in brief, is the answer.

But what makes a good model? I'll partially answer this question below, but in future posts I'll bring up specific examples of models, some good, some poor.

First, any "model" is a simplification of the reality. If the model is too simple, it won't be interesting. If it's too realistic, it will be too complex to understand. Thus, a good model is at that sweet spot where it's as simple as possible but no simpler.
Second, a model whose ingredients spell out the result you're looking for won't be interesting. Instead, the results should emerge from the combination of the model's resources, constraints and experience.

Third, a model with too many "free" parameters is less likely to be interesting. So an important requirement is that the "constraints" should be realistic, mimicking the constraints of the real system that is being modeled.

A common question I have gotten is: "Isn't a model just a way to fit inputs to outputs? Couldn't it just be replaced with a curve fitter or a regression?" Well, perhaps the answer should be yes IF you consider a human being to just be a curve fitting device. A human obtains inputs and generates outputs. So if you wish to say that a model is just a curve fitter, I will say that a human is, too.

What's interesting about neural systems, whether real or simulated, is the emergence of complex function from seemingly "simple" parts.

In future posts, I'll talk more about "constraints" by giving concrete examples. In the meantime, feel free to bring up any questions you have about the computational modeling of cognition.
-PL

[Image by Santiago Ramon y Cajal, 1914.]

The neural basis of preparation for willful action

My latest scientific publication is entitled Selection and maintenance of stimulus–response rules during preparation and performance of a spatial choice-reaction task (authors: Schumacher, Cole, and D'Esposito). It is a study using functional MRI with humans to investigate how we prepare for and execute willful action.

In this post I'll attempt to translate the article's findings for both the layperson and the uninitiated scientist.

What is willful action?

Willful action is a set of processes in direct contrast to automatic, habitual, processes. We can say with certainty that you are using willful action minimally when you are resting, brushing your teeth, driving to work for the thousandth time, or while performing any task that is effortless.

Willful action is necessary during two types of situations.

First, when you are attempting to do something for the first time (i.e., when you've had little practice at it) these processes are necessary for accurate performance. Think of the immense amount of effort while learning to drive. At first willful action was necessary, but later this need subsided.

Second, when two potential actions conflict in the brain willful action is necessary to overcome the incorrect action. The conflicting action may originate in an inappropriate desire, a habitual action that is no longer appropriate, or a natural tendency to perform one action rather than another.

In this latest publication we have used this last case (conflict due to a natural tendency to respond in a certain way) to investigate willful action.
Continue reading “The neural basis of preparation for willful action”

Pinker on ‘The Mystery of Consciousness’

Illustration for TIME by Istvan Orosz Time magazine has just published an intriguing article on the neural basis of consciousness. The article was written by Steven Pinker, a cognitive scientist known for his controversial views on language and cognition.

Here are several excerpts from the article…

On the brain being the basis for consciousness:

Scientists have exorcised the ghost from the machine not because they are mechanistic killjoys but because they have amassed evidence that every aspect of consciousness can be tied to the brain. Using functional MRI, cognitive neuroscientists can almost read people's thoughts from the blood flow in their brains.

On a new basis for morality emerging from neuroscience:

…the biology of consciousness offers a sounder basis for morality than the unprovable dogma of an immortal soul… once we realize that our own consciousness is a product of our brains and that other people have brains like ours, a denial of other people's sentience becomes ludicrous.

On the evolutionary basis of self deceit:

Evolutionary biologist Robert Trivers has noted that people have a motive to sell themselves as beneficent, rational, competent agents. The best propagandist is the one who believes his own lies, ensuring that he can't leak his deceit through nervous twitches or self-contradictions. So the brain might have been shaped to keep compromising data away from the conscious processes that govern our interaction with other people.

-MC

Wandering Minds and the Default Brain Network

Several news articles have come out today which seem to imply that a recent Science report's main finding is that the mind wanders for a purpose (see this Forbes article), and that "daydreaming improves thinking" (see this Cosmos article). These are typical of fabrications used by popular science journalists to pique the public's interest.

Mason, et al. 2007 (the Science article published today) did not say that the mind wanders for a purpose (though they speculated that there may be one), and specifically mentioned that "the mind may wander simply because it can". Also, I could not find anything about daydreaming improving thinking in the article, except a short sentence about daydreaming possibly improving arousal. (A slap to the face will probably improve arousal; will the next headline be "face slaps improve thinking"?)

The two popular news articles mentioned above present these very speculative statements from the article not only as fact but also as the main results of the research, which I find to be disingenuous.

As a researcher in the area, I would say these are the main points to take from Mason, et al. 2007:
Continue reading “Wandering Minds and the Default Brain Network”

Brainprints

Normally, neuroscientists try to discover things about the brain, as if it were one monolithic thing. Might the differences between individual brains be important, or useful?

A recent article in New Scientist describes recent efforts to use each person's unique brain activity patterns as a kind of fingerprint (or 'brainprint') for security purposes. The system uses EEG.

According to the article, "This novel biometric system should be difficult to forge, making it suitable for high-security applications". I'm trying to imagine a CIA operative putting on a little red EEG cap before being allowed into a top secret location…

-MC

Can a Neural Network be Free…

…from a knee-jerk reaction to its immediate input?

Although one of the first things that a Neuroscience student learns about is "reflex reactions" such as the patellar reflex (also known as the knee-jerk reflex), the cognitive neuroscientist is interested in the kind of processing that might occur between inputs and outputs in mappings that are not so direct as the knee-jerk reaction.

An example of a system which is a step up from the knee-jerk reflex is in the reflexes of the sea slug named "Aplysia". Unlike the patellar reflex, Aplysia's gill and siphon retraction reflexes seem to "habituate" over time — the original input-output mappings are overridden by being repeatedly stimulated. This is a simple form of memory, but no real "processing" can be said to go on there.

Specifically, cognitive neuroscientists are interested in mappings where "processing" seems to occur before the output decision is made. As MC pointed out earlier, the opportunity for memory (past experience) to affect those mappings is probably important for "free will".

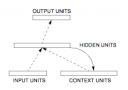
But how can past experience affect future mappings in interesting ways? One answer to this question appeared in the year 1990, which began a new era in experimentation with neural network models capable of indirect input-output mappings. In that year, Elman (inpired by Jordan's 1986 work) demonstrated the Simple Recurrent Network in his paper "Finding Structure in Time". The concept behind this network is shown in the picture associated with this entry.

The basic idea of the Simple Recurrent Network is that as information comes in (through the input units), an on-line memory of that information is preserved and recirculated (through the "context" units). Together, the input and context units both influence the hidden layer which can trigger responses in the output layer. This means that the immediate output of the network is dependent not only on the current input, but also on the inputs that came before it.

The most interesting aspect of the Simple Recurrent Network, however, is that the connections among all the individual units in the network change depending on what the modeler requires the network to output. The network learns to preserve information in the context layer loops so that it can correctly produce the desired output. For example, if the task of the network is to remember the second word in a sentence, it will amplify or maintain the second word when it comes in, while ignoring the intervening words, so that at the end of the sentence it outputs the target word.

Although this network cannot be said to have "free" will — especially because of the way its connections are forcefully trained — its operation can hint at the type of phenomena researchers should seek in trying to understand cognition in neural systems.

-PL

The Will to be Free, Part I

Freedom to choose is the first axiom of our being. We assume freedom with each action that we take, and we are annoyed when we are forced to act "against our will". A recent article on free will at the New York Times explains that determinism is a direct implication of the brain being the seat of the mind in conjunction with Newtonian physics (also see the recent Mind Hacks post). Why, then, do we assume at each moment that we have free will? How is it that someone could use force and coercion to take away a freedom that we never had to begin with?

An increasingly common argument against determinism is based in quantum physics. Certainly Newtonian physics (where every cause must have a pre-determined effect) implies determinism, the argument goes, but quantum physics allows for some 'wiggle room'. Such wiggling takes place at the subatomic level in the form of random movements, such that events in the world supposedly have a base of random chance behind them.

I actually find quantum physics to be a negative for free will: I would rather have a predictable and determined will than one that was based on a series of coin flips. At least a determined will allows for the maintenance of a self that can choose (even if the same decision is made every time).

But why don't we make the same decision every time? Because we have memory.
Continue reading “The Will to be Free, Part I”

Neuroscience Blogs of Note, Part 2

I will follow up MC's recent post with a brief review of three other neuroscience-related blogs that are worth mentioning as we begin Neurevolution.
Brain Waves (http://brainwaves.corante.com/) is a self-labeled "neurotechnology" blog. Written by Zack Lynch, it is a real-world look at the effects and benefits derived from neuroscience research with regards to society, culture and economics. The author has a background in evolutionary biology but brings to light articles spanning a wide range of topics including neuroeconomics, nanotechnology, pharmaceutical research, perceptual illusions, and music appreciation. The focus of the blog however is on neurotechnology — on technological advancements that permit the improvement or study of the brain.

SCLin's Neuroscience Blog (http://forebrain.blogspot.com/) contains pointers to and summaries of recent neuroscience articles which focus on computational and cognitive neuroscience issues. While too technical to be of much value to the layperson, it reports on articles dealing with cutting-edge questions in neuroscience, such as the nature of the information code in the brain (e.g. meaningful representations in the prefrontal cortex) and information flow through neural pathways (e.g. the short-latency activation of dopaminergic neurons by visual stimuli).

Although It may be hard to classify as a neuroscience blog, Neurophilosophy (http://neurophilosophy.wordpress.com/) does contain a fair number of interesting posts for the neuroscientist, such as a recent one on mind-computer interfaces for robots. Recent articles however have focused more on topics as varied as biological mimicry, hibernation, bionic hands, animals that blow bubbles to smell underwater, and other non-neuroscience topics. As such, it focuses on fascinating science questions in general, of which neuroscience is certainly a part.

This ends our first review. Stay tuned for further reviews, as well as new content and pointers to other interesting articles!

-PL

Neuroscience Blogs of Note

As the first post on Neurevolution, I would like to review several other neuroscience blogs that have been around for a while.

First is Mind Hacks, a blog by the two authors of the book by the same name. According to the authors, the blog and book include "neuroscience and psychology tricks to find out what's going on inside your brain". Many of the topics covered are very similar to those that will be covered here: issues at the edge of cognition and neuroscience.

A post of particular interest simply quoted Marvin Minsky (a prominent figure in the field of artificial intelligence) from his book Society of Mind.

People ask if machines have souls. And I ask back whether souls can learn. It does not seem a fair exchange – if souls can live for endless time and yet not use that time to learn – to trade all change for changelessness.

…

What are those old and fierce beliefs in spirits, souls, and essences? They're all insinuation that we're helpless to improve ourselves. To look for our virtues in such thoughts seems just as wrongly aimed a search as seeking art in canvas cloths by scraping off the painter's works.

I found this quote very moving, as it expresses (by comparison) the wonderful joy of learning and change. It's also profound because it questions certain long-held assumptions about what immortality would be like, and what we would want it to be like.

Another post of interest explained how the retina ("the only part of the central nervous system visible from outside the body") and associated structures can reveal a great deal about cognitive functions. It turns out that as items are stored in working memory the pupil dilates (more with each successive item), and as the items are recalled and repeated back to the experimenter the pupil contracts down to its normal size. What does this say about system integration in the brain? It likely means that even low-level regions controlling pupil dilation or eye-movement initiation are tied intimately with regions involved in higher level cognition such as working memory.
Continue reading “Neuroscience Blogs of Note”